It’s March, which means March Madness for fans of college basketball.
Mathnasium recently joined CBS to discuss March Mathness - the statistics that go into building the perfect bracket for the tournament! You can check out the segment here.
What is March Madness?
March Madness is the NCAA Basketball playoffs; 64 of the nation’s leading division 1 basketball teams face off to be titled the Championship Team for the season. The 64 teams are arranged in a bracket, with teams placed in seeds based on location and regular season performance. The team ranked #1 in their region will play their first game against #16, #2 will play #15, #3 plays #14, so on and so forth. Teams are narrowed down by the process of elimination until one team is left victorious.
It’s great fun for basketball fans to try and predict the outcome of the 63 games that take place during the tournament by filling out their bracket. Brackets start with all 64 teams and participants will select which team they assume will advance in a single-elimination game to the next round.
This annual contest amongst friends is far more challenging than it may seem, however, because predicting the perfect bracket is near impossible. To be exact, the chances of correctly predicting every outcome accurately, is 1 in 9,223,372,036,854,775,808 (that's 9.2 quintillion).
Why is Predicting the Perfect Bracket Nearly Impossible?
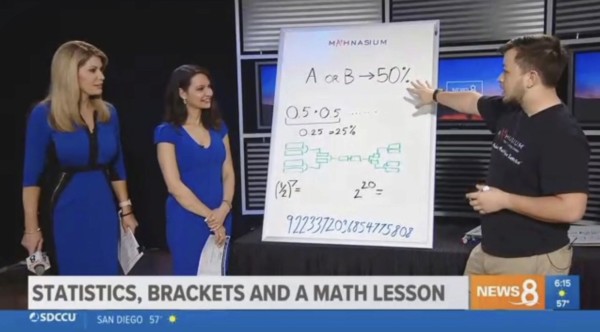 Let’s answer this by simply with the equation for the probability you guess the outcome correctly. In a game with only two teams, there is a 50/50 shot a team will win (this of course is a gross oversimplification, but more on that later).
Let’s answer this by simply with the equation for the probability you guess the outcome correctly. In a game with only two teams, there is a 50/50 shot a team will win (this of course is a gross oversimplification, but more on that later).
So our odds of guessing the outcome of 1 game is 50%. When determining the probability of multiple events occurring, you multiply the probability of Event 1 occurring by the probability of Event 2 occurring. For this example, let’s say the probability of assuming the outcome of the game between seed #1 and seed #16 is 50%, and the probability of assuming the outcome of the game between #2 and #15 is 50%, then the likelihood of predicting both game outcomes correctly is 25% because .5 times .5 is .25.
If we follow this same equation for simply predicting the correct outcomes for all the games in the Round of 64, the likelihood of getting a perfect bracket is 1 in 4,294,967,296. And we will have 5 rounds left!
By the time you make it to the Championship, the likelihood of having a perfect bracket is 1 in 9,223,372,036,854,775,808, because (0.5)^63 equals 1/9,223,372,036,854,775,808.
What Else Makes Probable Outcomes Impossible to Predict?
In real world applications, the likelihood of predicting the outcome of a basketball game isn’t 50/50.
This is for many reasons:
- Injuries
- Home court advantage
- Experience
- Seed rank
- Rivalries
With these differences in percentages showing one team winning as a favorable outcome, more bracket users are inclined to select that team to advance. When the team who has winning the game in their favor gets defeated, however, then you have an Upset and many brackets are destroyed.
 With so many factors at play, bracketology is an impossible statistical mess. Which is probably why Warren Buffet offered to give 1 million dollars for life to any of his employees who managed to fill out their Sweet 16 bracket perfectly.
With so many factors at play, bracketology is an impossible statistical mess. Which is probably why Warren Buffet offered to give 1 million dollars for life to any of his employees who managed to fill out their Sweet 16 bracket perfectly.
Enjoy watching the remainder of March Madness! Hopefully there will be more awesome bracket breakers to come!








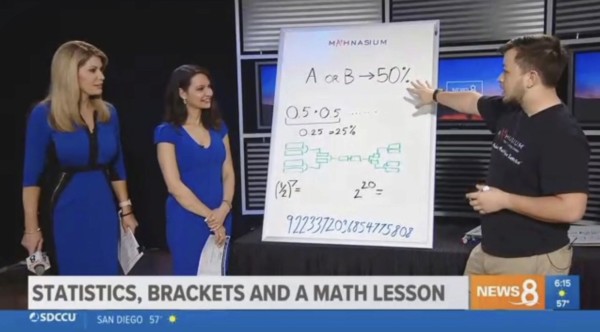 Let’s answer this by simply with the equation for the probability you guess the outcome correctly. In a game with only two teams, there is a 50/50 shot a team will win (this of course is a gross oversimplification, but more on that later).
Let’s answer this by simply with the equation for the probability you guess the outcome correctly. In a game with only two teams, there is a 50/50 shot a team will win (this of course is a gross oversimplification, but more on that later).


