People ask us why we play math games at a Math Learning Center. Read this article from the National Council of Teachers of Mathematics
http://www.nctm.org/publications/teaching-children-mathematics/blog/why-play-math-games_/
By Kitty Rutherford, Posted April 27, 2015 –
People of all ages love to play games that are fun and motivating. Games give students opportunities to explore fundamental number concepts, such as the counting sequence, one-to-one correspondence, and computation strategies. Engaging mathematical games can also encourage students to explore number combinations, place value, patterns, and other important mathematical concepts. Further, they afford opportunities for students to deepen their mathematical understanding and reasoning. Teachers should provide repeated opportunities for students to play games, then let the mathematical ideas emerge as students notice new patterns, relationships, and strategies. Games are an important tool for learning in elementary school mathematics classrooms:
• Playing games encourages strategic mathematical thinking as students find different strategies for solving problems and deepen their understanding of numbers.
• When played repeatedly, games support students’ development of computational fluency.
• Games present opportunities for practice, often without the need for teachers to provide the problems. Teachers can then observe or assess students and work with individuals or small groups of students.
• Games have the potential to allow students to develop familiarity with the number system and with “benchmark numbers” (such as 10s, 100s, and 1000s) and engage in computation practice, building a deeper understanding of operations.
• Games support a school-to-home connection. Parents can learn about their children’s mathematical thinking by playing games with them at home.

This game is on p. 65 of the downloadablePDF.
Building Fluency
Fluency requires a balance and connection between conceptual understanding and computational proficiency. Computational methods that are over-practiced without understanding are forgotten or remembered incorrectly. Conceptual understanding without fluency can inhibit the problem-solving process (NCTM 2000, Principles and Standards for School Mathematics, p. 35).
Developing computational fluency is an expectation of the Common Core State Standards for Mathematics. Games provide opportunity for meaningful practice. The research about how students develop fact mastery indicates that drill techniques and timed tests do not have the power that mathematical games and other experiences have. Appropriate mathematical activities are essential building blocks to develop mathematically proficient students who demonstrate computational fluency (Van de Walle and Lovin, Teaching Student-Centered Mathematics Grades K–3, p. 94). Remember, computational fluency includes efficiency, accuracy, and flexibility with strategies (Russell 2000).
The kinds of experiences that teachers offer their students clearly play a major role in determining the extent and quality of students’ learning. Students can build understanding by actively engaging in tasks and experiences designed to deepen and connect their knowledge. Procedural fluency and conceptual understanding can be developed through problem solving, reasoning, and argumentation (NCTM 2000, Principles and Standards for School Mathematics, p. 21). Meaningful practice is necessary to develop fluency with basic number combinations and strategies with multidigit numbers. Practice should be purposeful and should focus on developing thinking strategies and a knowledge of number relationships rather than on drilling isolated facts (NCTM 2000, Principles and Standards for School Mathematics, p. 87). Do not subject any student to computation drills unless the student has developed an efficient strategy for the facts included in the drill (Van de Walle and Lovin 2006, Teaching Student-Centered Mathematics Grades K–3, p. 117). Drills can strengthen strategies with which students feel comfortable—those they “own”—and will help make these strategies increasingly automatic. Therefore, strategy drills will allow students increasing efficiency, even to the point of recalling a fact without being conscious of using a strategy. Drills without an efficient strategy offer no assistance (Van de Walle and Lovin 2006, Teaching Student-Centered Mathematics Grades K–3, p. 117).

This game is on p. 5 of the downloadable PDF.
Cautions
Sometimes teachers use games solely to practice number facts. These games usually do not engage children for long because they are based on students’ recall or memorization of facts. Some students are quick to memorize; others need a few moments to compute a related fact. When students are placed in situations in which recall speed determines success, they may infer that being “smart” in mathematics means getting the correct answer quickly instead of valuing the process of thinking. Consequently, students may feel incompetent when they use number patterns or related facts to arrive at a solution and may begin to dislike mathematics because they are not fast enough.

This game is on p. 67 of the downloadable PDF.
Introduce a game
A good way to introduce a game to the class is for the teacher to play the game against the class. After briefly explaining the rules, ask students to make the class’s next move. Teachers may also want to model their strategy by talking aloud for students to hear his or her thinking. “I placed my game marker on the six because that would give me the largest number.”
Games are fun and can create a context for developing students’ mathematical reasoning. Through playing and analyzing games, students also develop their computational fluency by examining strategies that are more efficient and by discussing relationships among numbers. Teachers can create opportunities for students to explore mathematical ideas by planning questions that prompt students to reflect about their reasoning and make predictions. Remember to always vary or modify the game to meet the needs of your leaners. Encourage the use of the Common Core’s Standards for Mathematical Practice.
Holding Students Accountable
While playing games, have students record mathematical equations or representations of the mathematical tasks. This yields data for students and teachers to revisit to examine their mathematical understanding.
After playing a game, have students reflect on the game by asking them to discuss questions orally or write about them in a mathematics notebook or journal:
• What skill did you review and practice?
• Which strategies did you use while playing the game?
• If you were to play the games a second time, what different strategies would you use to be more successful?
• How could you tweak or modify the game to make it more challenging?
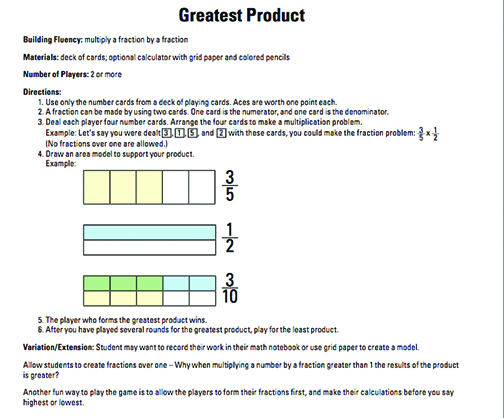
This game is on p. 42 of the downloadable PDF.

K–Grade 5 Math Games were created by North Carolina teachers and can be accessed on the North Carolina Department of Public Instruction,
under Kindergarten Instructional Resources/Games.
For students to become fluent in arithmetic computation, “they must have efficient and accurate methods that are supported by an under-standing of numbers and operations. ‘Standard’ algorithms for arithmetic computation are one means of achieving this fluency” (NCTM 2000, Principles and Standards for School Mathematics, p. 35).
“Overemphasizing fast fact recall at the expense of problem solving and conceptual experiences gives students a distorted idea of the nature of mathematics and of their ability to do mathematics” (Seeley 2009, Faster Isn’t Smarter: Messages about Math, Teaching, and Learning in the 21st Century, p. 95).
“Fluency refers to having efficient, accurate, and generalizable methods (algorithms) for computing that are based on well-understood properties and number relationships” [emphasis mine] (NCTM 2000, Principles and Standards for School Mathematics, p. 144).
“Computational fluency refers to having efficient and accurate methods for computing. Students exhibit computational fluency when they demonstrate flexibility in the computational methods they choose, understand and can explain these methods, and produce accurate answers efficiently” [emphasis mine] (NCTM 2000, Principles and Standards for School Mathematics, p. 152).
 Kitty Rutherford serves as the North Carolina Elementary Mathematics Consultant for the Department of Public Instruction in Raleigh. She is an experienced leader, collaborator, and licensed educator with a Master’s Degree in Elementary Education coupled with over twenty-seven years’ experience teaching elementary school students, training educators, collaborating with multiple stake-holders, and implementing effective programs. She has received such honors as the Presidential Award for Excellence in Mathematics and Science Teaching, NCCTM Outstanding Elementary Mathematic Teacher, Alpha Delta Kappa State Excellence in Education Award, and Teacher of the Year Finalist. She currently serves as the State Coordinator for the NC Presidential Award for Excellence in Mathematics Teaching and on the board of the North Carolina Council of Teachers of Mathematics.
Kitty Rutherford serves as the North Carolina Elementary Mathematics Consultant for the Department of Public Instruction in Raleigh. She is an experienced leader, collaborator, and licensed educator with a Master’s Degree in Elementary Education coupled with over twenty-seven years’ experience teaching elementary school students, training educators, collaborating with multiple stake-holders, and implementing effective programs. She has received such honors as the Presidential Award for Excellence in Mathematics and Science Teaching, NCCTM Outstanding Elementary Mathematic Teacher, Alpha Delta Kappa State Excellence in Education Award, and Teacher of the Year Finalist. She currently serves as the State Coordinator for the NC Presidential Award for Excellence in Mathematics Teaching and on the board of the North Carolina Council of Teachers of Mathematics.

 877-601-6284
877-601-6284 877-601-6284
877-601-6284








 Kitty Rutherford serves as the North Carolina Elementary Mathematics Consultant for the Department of Public Instruction in Raleigh. She is an experienced leader, collaborator, and licensed educator with a Master’s Degree in Elementary Education coupled with over twenty-seven years’ experience teaching elementary school students, training educators, collaborating with multiple stake-holders, and implementing effective programs. She has received such honors as the Presidential Award for Excellence in Mathematics and Science Teaching, NCCTM Outstanding Elementary Mathematic Teacher, Alpha Delta Kappa State Excellence in Education Award, and Teacher of the Year Finalist. She currently serves as the State Coordinator for the NC Presidential Award for Excellence in Mathematics Teaching and on the board of the North Carolina Council of Teachers of Mathematics.
Kitty Rutherford serves as the North Carolina Elementary Mathematics Consultant for the Department of Public Instruction in Raleigh. She is an experienced leader, collaborator, and licensed educator with a Master’s Degree in Elementary Education coupled with over twenty-seven years’ experience teaching elementary school students, training educators, collaborating with multiple stake-holders, and implementing effective programs. She has received such honors as the Presidential Award for Excellence in Mathematics and Science Teaching, NCCTM Outstanding Elementary Mathematic Teacher, Alpha Delta Kappa State Excellence in Education Award, and Teacher of the Year Finalist. She currently serves as the State Coordinator for the NC Presidential Award for Excellence in Mathematics Teaching and on the board of the North Carolina Council of Teachers of Mathematics.











