877-601-6284
US
CA
UK
See Our Method 
OUR RESULTS
The results are transformative - families will see measurable changes in attitude, confidence, and school progress.
See Our ResultsFor decades the Mathnasium Method™ has transformed the way kids learn math. We build a foundation for math mastery through deep understanding by starting with what they already know, addressing any learning gaps, expanding their mathematical thinking, and adding new concepts in sequence. This proprietary method works for kids of all ages and skill levels, whether they’re struggling in math, doing okay but could be doing better, or are already excelling but need more of a challenge. When kids see what they can achieve because of their proficiency in math, it can alter the course of their entire lives.
We take our students on a journey of learning – through assessment, customized learning paths and targeted lessons for understanding and comprehension.
We begin with a comprehensive assessment, which includes both a verbal and written component, to pinpoint their exact strengths and weaknesses.
This plan is created for each child based on their assessment, so they will truly learn and grow in their mathematical thinking.
Our expert instructors don’t just teach student to memorize or calculate; they teach them to truly understand the way math works.
As students achieve their goals, they are reassessed and move on to new challenges.
This is the key to success in math—the understanding of what numbers mean and how they work together. And Number Sense isn't just for young kids. We work on these topics through the levels shown below before moving on to Algebra and other higher math disciplines.
Counting is the key to unlocking addition and subtraction in early math development. At Mathnasium, our initial goal is to have a student become comfortable with counting to any number, from any number, by any number, forward and backwards.
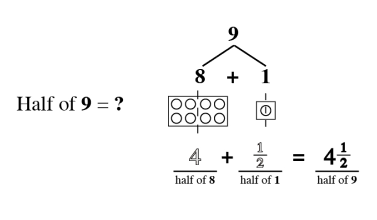
As students begin to understand the relationship between a whole and the parts, a world of mathematical concepts and exercises can be explored. Once students have mastered these skills, they have little trouble with algebraic problem-solving.
The quantity and denomination construct examine two aspects of numerical value. Quantity asks “how many” and denomination asks “of what.”
Proportional thinking establishes a fundamental base that leads to a stronger understanding of critical concepts like ratios, direct and indirect variation, and algebraic reasoning.
The Law of SAMEness is a concept students naturally apply in their reasoning without being aware of it. For example, quantities of apples and bananas cannot be added together unless first being changed so that they have the same name, which is fruit.
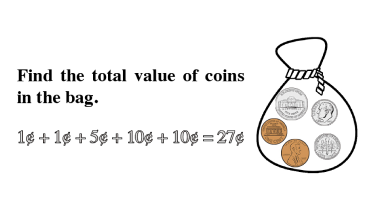
Counting is the key to unlocking addition and subtraction in early math development. At Mathnasium, our initial goal is to have a student become comfortable with counting to any number, from any number, by any number, forward and backwards.
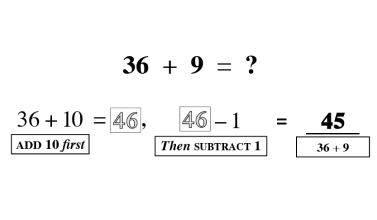
As students begin to understand the relationship between a whole and the parts, a world of mathematical concepts and exercises can be explored. Once students have mastered these skills, they have little trouble with algebraic problem-solving.
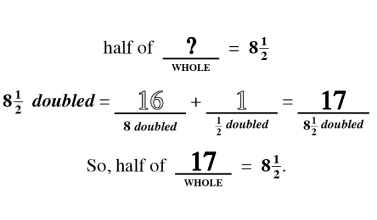
The quantity and denomination construct examine two aspects of numerical value. Quantity asks “how many” and denomination asks “of what.”
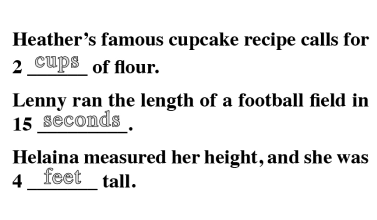
Proportional thinking establishes a fundamental base that leads to a stronger understanding of critical concepts like ratios, direct and indirect variation, and algebraic reasoning.
The Law of SAMEness is a concept students naturally apply in their reasoning without being aware of it. For example, quantities of apples and bananas cannot be added together unless first being changed so that they have the same name, which is fruit.
Counting is the key to unlocking addition and subtraction in early math development. At Mathnasium, our initial goal is to have a student become comfortable with counting to any number, from any number, by any number, forward and backwards.
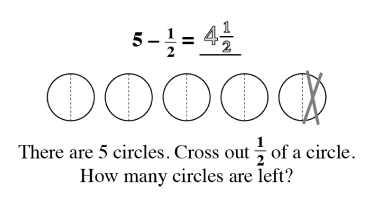
As students begin to understand the relationship between a whole and the parts, a world of mathematical concepts and exercises can be explored. Once students have mastered these skills, they have little trouble with algebraic problem-solving.
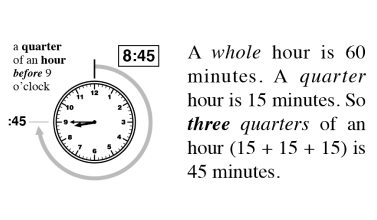
The quantity and denomination construct examine two aspects of numerical value. Quantity asks “how many” and denomination asks “of what.”
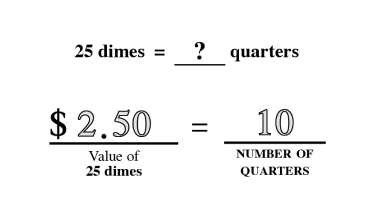
Proportional thinking establishes a fundamental base that leads to a stronger understanding of critical concepts like ratios, direct and indirect variation, and algebraic reasoning.
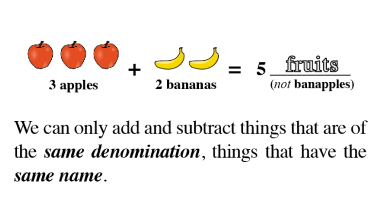
The Law of SAMEness is a concept students naturally apply in their reasoning without being aware of it. For example, quantities of apples and bananas cannot be added together unless first being changed so that they have the same name, which is fruit.
Counting is the key to unlocking addition and subtraction in early math development. At Mathnasium, our initial goal is to have a student become comfortable with counting to any number, from any number, by any number, forward and backwards.
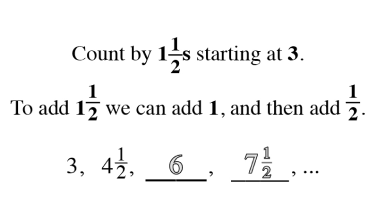
As students begin to understand the relationship between a whole and the parts, a world of mathematical concepts and exercises can be explored. Once students have mastered these skills, they have little trouble with algebraic problem-solving.
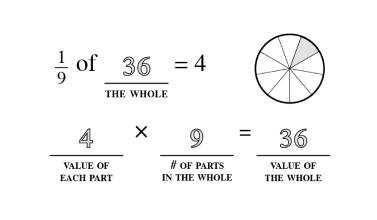
The quantity and denomination construct examine two aspects of numerical value. Quantity asks “how many” and denomination asks “of what.”
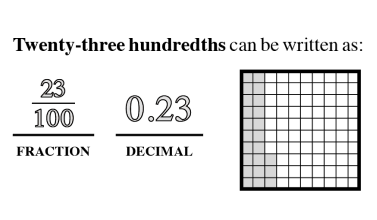
Proportional thinking establishes a fundamental base that leads to a stronger understanding of critical concepts like ratios, direct and indirect variation, and algebraic reasoning.
The Law of SAMEness is a concept students naturally apply in their reasoning without being aware of it. For example, quantities of apples and bananas cannot be added together unless first being changed so that they have the same name, which is fruit.
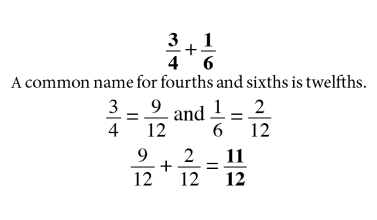
Counting is the key to unlocking addition and subtraction in early math development. At Mathnasium, our initial goal is to have a student become comfortable with counting to any number, from any number, by any number, forward and backwards.
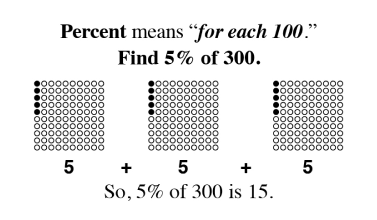
As students begin to understand the relationship between a whole and the parts, a world of mathematical concepts and exercises can be explored. Once students have mastered these skills, they have little trouble with algebraic problem-solving.
The quantity and denomination construct examine two aspects of numerical value. Quantity asks “how many” and denomination asks “of what.”
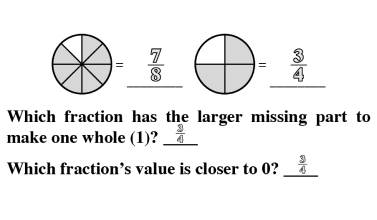
Proportional thinking establishes a fundamental base that leads to a stronger understanding of critical concepts like ratios, direct and indirect variation, and algebraic reasoning.
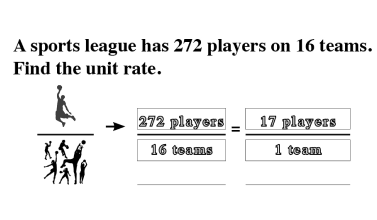
The Law of SAMEness is a concept students naturally apply in their reasoning without being aware of it. For example, quantities of apples and bananas cannot be added together unless first being changed so that they have the same name, which is fruit.
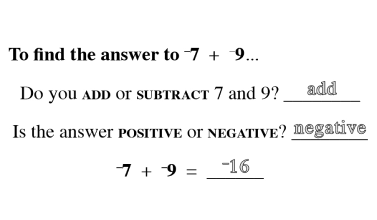
Counting is the key to unlocking addition and subtraction in early math development. At Mathnasium, our initial goal is to have a student become comfortable with counting to any number, from any number, by any number, forward and backwards.
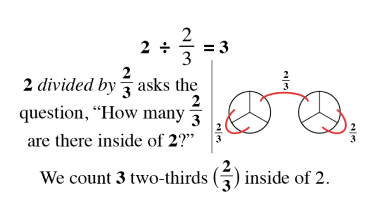
As students begin to understand the relationship between a whole and the parts, a world of mathematical concepts and exercises can be explored. Once students have mastered these skills, they have little trouble with algebraic problem-solving.
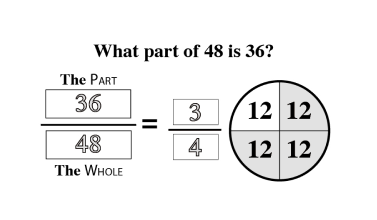
The quantity and denomination construct examine two aspects of numerical value. Quantity asks “how many” and denomination asks “of what.”
Proportional thinking establishes a fundamental base that leads to a stronger understanding of critical concepts like ratios, direct and indirect variation, and algebraic reasoning.
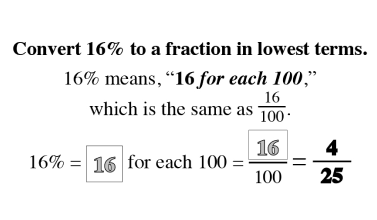
The Law of SAMEness is a concept students naturally apply in their reasoning without being aware of it. For example, quantities of apples and bananas cannot be added together unless first being changed so that they have the same name, which is fruit.
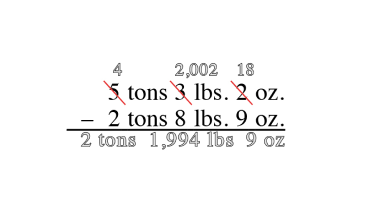
Counting is the key to unlocking addition and subtraction in early math development. At Mathnasium, our initial goal is to have a student become comfortable with counting to any number, from any number, by any number, forward and backwards.
As students begin to understand the relationship between a whole and the parts, a world of mathematical concepts and exercises can be explored. Once students have mastered these skills, they have little trouble with algebraic problem-solving.
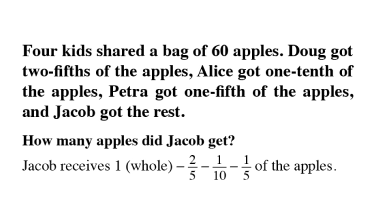
The quantity and denomination construct examine two aspects of numerical value. Quantity asks “how many” and denomination asks “of what.”
Proportional thinking establishes a fundamental base that leads to a stronger understanding of critical concepts like ratios, direct and indirect variation, and algebraic reasoning.
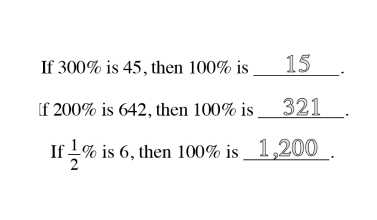
The Law of SAMEness is a concept students naturally apply in their reasoning without being aware of it. For example, quantities of apples and bananas cannot be added together unless first being changed so that they have the same name, which is fruit.
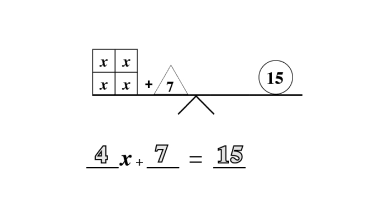
Counting is the key to unlocking addition and subtraction in early math development. At Mathnasium, our initial goal is to have a student become comfortable with counting to any number, from any number, by any number, forward and backwards.
As students begin to understand the relationship between a whole and the parts, a world of mathematical concepts and exercises can be explored. Once students have mastered these skills, they have little trouble with algebraic problem-solving.
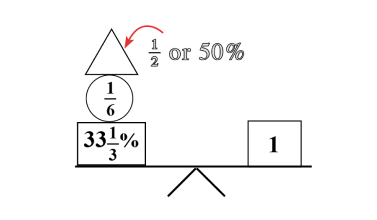
The quantity and denomination construct examine two aspects of numerical value. Quantity asks “how many” and denomination asks “of what.”
Proportional thinking establishes a fundamental base that leads to a stronger understanding of critical concepts like ratios, direct and indirect variation, and algebraic reasoning.
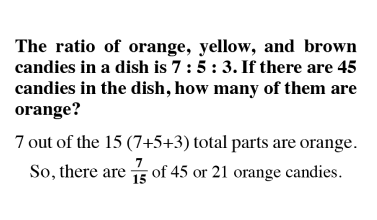
The Law of SAMEness is a concept students naturally apply in their reasoning without being aware of it. For example, quantities of apples and bananas cannot be added together unless first being changed so that they have the same name, which is fruit.
We use a combination of mental, verbal, visual, tactile, and written techniques to build math knowledge level by level, so they understand it, master it, and enjoy it.
The results are transformative - families will see measurable changes in attitude, confidence, and school progress.
See Our Resultsof parents report an improvement in their child’s math skills and understanding.
of parents report improved attitude toward math after attending Mathnasium.
of students saw an improvement in their school grades.
Math went from being a seemingly insurmountable challenge for our son to being one of his strongest subjects in school.
Loreana C., Parent, Newton Center
Huge progress on my 3rd grade kid's math skills in matter of few weeks. Very helpful and friendly staff. I'm ...
My daughter had a really challenging year with math in her freshman year. She started Mathnasium sometime in A...
We have nearly 1,000 centers nationwide. Get started now.
