November 23 is Fibonacci Day, commemorating the Italian mathematician Leonardo of Pisa and the pattern of numbers he popularized, the Fibonacci sequence. Observing the beginning of this sequence, you will notice why we celebrate on this day: 0, 1, 1, 2, 3, 5, 8, 13, …
Written in the date format month/day, you see the date 11/23 or November 23.
Fibonacci Sequence
Leonardo of Pisa (c. 1170-1250), nicknamed “Fibonacci,” introduced this number sequence to the Western World during the Middle Ages. But he was not the first to observe this special pattern of numbers. As early as 200 B.C., the sequence appeared in mathematics from India.
Fibonacci shared the interesting mathematical properties of this sequence in his “Book of Calculation,” which he had gathered from early life travels to North Africa. It wasn’t until the late 1800s that the series was named after Fibonacci as a tribute to his work!
A number sequence is an ordered list of numbers defined by a rule or function — in other words, a pattern. Each number in the sequence is called a term.
It may be challenging to determine the rule for the Fibonacci sequence when looking at what is happening in between each number; unlike most numeral patterns that we learn as kids, the change is different. To find the rule, look at the numbers themselves.
Rule: To get to the next term, add the two previous terms together.
The Fibonacci sequence is infinite since it has an unlimited number of terms and goes on indefinitely.
A Cool Math Fact: Begin the sequence with 1. From here, every third term is divisible by 2; every fourth term is divisible by 3; every fifth term is divisible by 5; every sixth term is divisible by 8; every seventh term is divisible by 13; and so on.
Example:
Every third term of the sequence is: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …
These terms are all divisible by 2.
Every fourth term of the sequence is: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …
These terms are all divisible by 3.
Every fifth term of the sequence is: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …
These terms are all divisible by 5.
Fibonacci Numbers in the Real World
Fascination with the Fibonacci sequence of numbers extends beyond mathematics. This pattern appears quite frequently in nature and the real world!
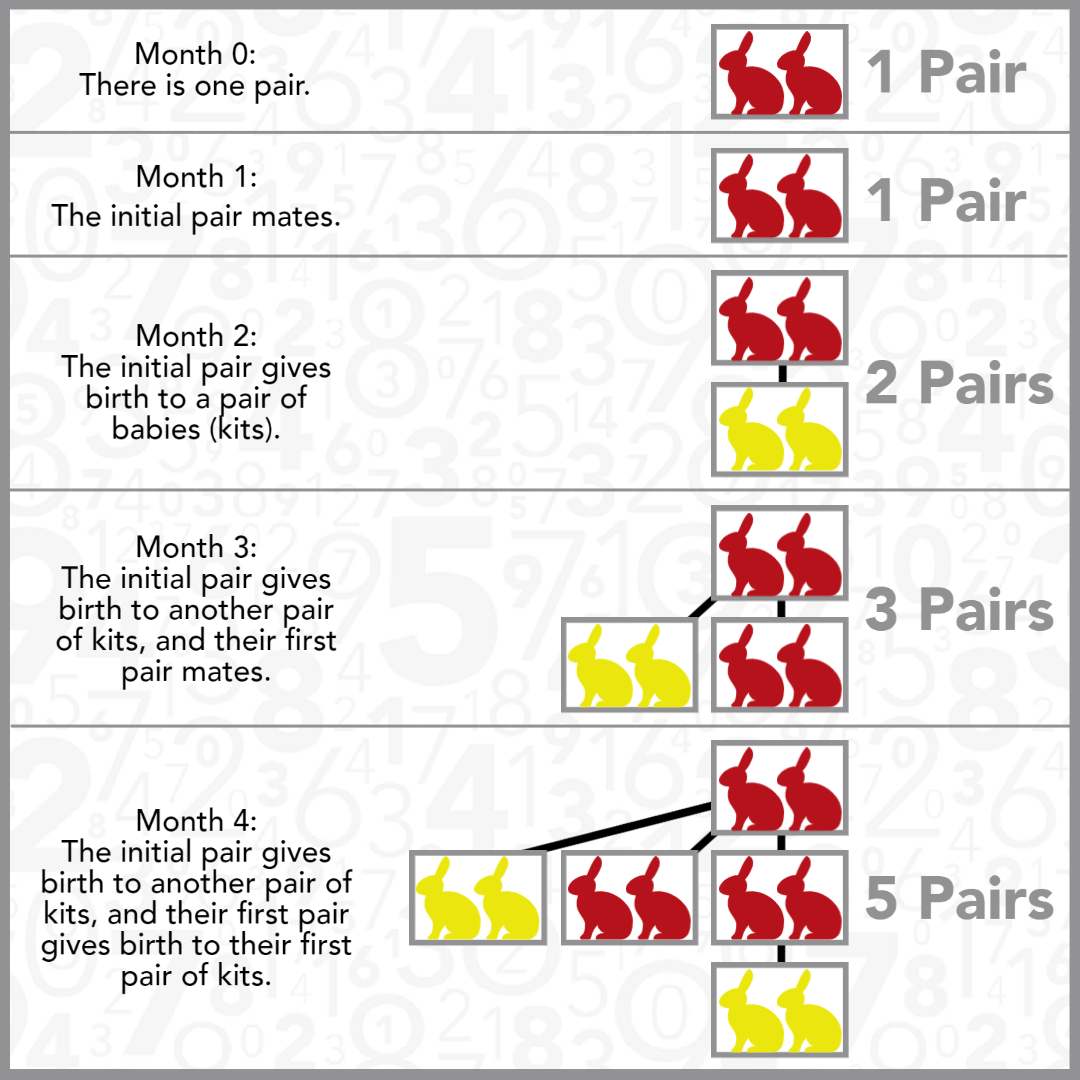
When Leonardo of Pisa first presented the sequence, he posed a population-growth scenario with rabbits. The overall problem showed that after each month, the number of pairs of rabbits increased following the Fibonacci pattern.
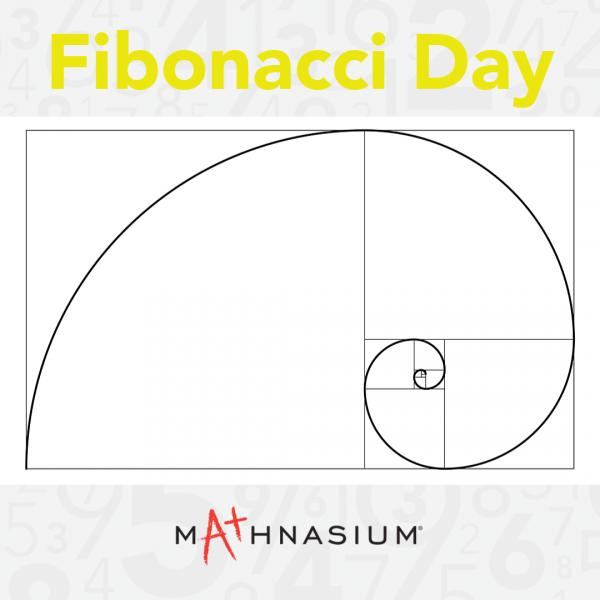
From flower petals to pineapples, many elements in nature follow some portion of the Fibonacci sequence. Fibonacci numbers can be turned into tiles (the terms dictate the side lengths of each square), and a Fibonacci Spiral can be constructed by connecting the opposite corners of the squares. This spiral is easy to spot in natural settings, for example, the spiral arrangement on pinecones; the numbers of spirals correspond to Fibonacci numbers. In this example, we see 8 spirals counted clockwise and 13 spirals counted counter-clockwise!

The Fibonacci sequence is also used in computer algorithms, architecture, and design. If you divide pairs of consecutive terms in the sequence, the quotients (or ratios), move closer and closer to the irrational number phi (approximately 1.6), otherwise known as the Golden Ratio. Artists have long found this ratio to present the most aesthetically pleasing art.
We’re sure Fibonacci would agree: Math is so cool! The Fibonacci sequence shows us that even within one unique number pattern, there are so many things going on! Take some time today to explore more patterns around you.
To learn more about patterns, reach out to your nearest Mathnasium Learning Centre.

 877-601-6284
877-601-6284 877-601-6284
877-601-6284