Regardless of age or skill level, there are almost always gaps in a child’s foundational understanding that, if addressed, would boost their success in math.
When we give assessments to children in our math learning centers, we see that a high proportion of their knowledge gaps stems from a lack of number sense. Number sense is “the ability to appreciate the size and scale of numbers in the context of the question at hand.” In essence, it’s the understanding of what numbers mean, how they work together and how they connect to real life. It’s critical that children have a firm grasp of number sense, because it underlies all mathematical comprehension and ability. Typical math tutoring does not teach number sense, acting as a bandage rather than a cure for the problem.
How do I know if my child has number sense?
Context provides a framework of ideas and information that can be used in a meaningful way. If a child doesn’t understand the context of a mathematical concept or principle when it’s taught to them, they’re likely to say they “don’t get it” or that it “doesn’t make sense.” Sound familiar?
Without number sense, a child feels increasingly lost as they move up through the school grades. Year after year, the disparity grows between what they are being taught and what they truly understand. Children who lack number sense work longer and harder than they should have to in order to solve math problems. Students in middle- and high-school-level math courses — even if they seem to be doing OK — can still lack number sense, because they never got a good grip on it when they were younger. This is part of why so many children need a math tutor.
Children who have good number sense are able to solve problems like these quickly in their heads:
What is 7% of 250?
99 + 99 + 99 = ?
Which is the largest? 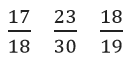
Whether it’s in the early or later years, eventually, the child without number sense will “hit a wall.” This can manifest as the inability to understand new material, do certain types of problems, low grades on timed tests, homework frustration, or the mistaken belief that they “can’t do math.” In fact, it’s often problems with number sense that cause children to give up on math. It’s a pity, because it doesn’t have to be that way. Anyone, of any age, can be taught number sense! It’s never too late to learn.
How do we learn number sense?
The important thing to realize is that number sense doesn’t just come naturally. It’s a learned skill. Teachers can instill number sense if they have the right materials (curriculum and tools) and use the right instruction. This is why Mathnasium invested 40+ years and millions of dollars refining the Mathnasium Method™. By teaching number sense in a way that makes sense to children, Mathnasium supports children’s classroom education.
In addition to teachers, parents and other caregivers also play a role in children’s mathematical growth. It’s often as simple as spending a few minutes each day asking number sense-related questions. You can do this on the way to and from school, at the market, or even when enjoying a sporting event together. It’s a great way to instill in your child that math is an important part of everyday life. For great tips on how to do this, see this article.
What are the components of number sense?
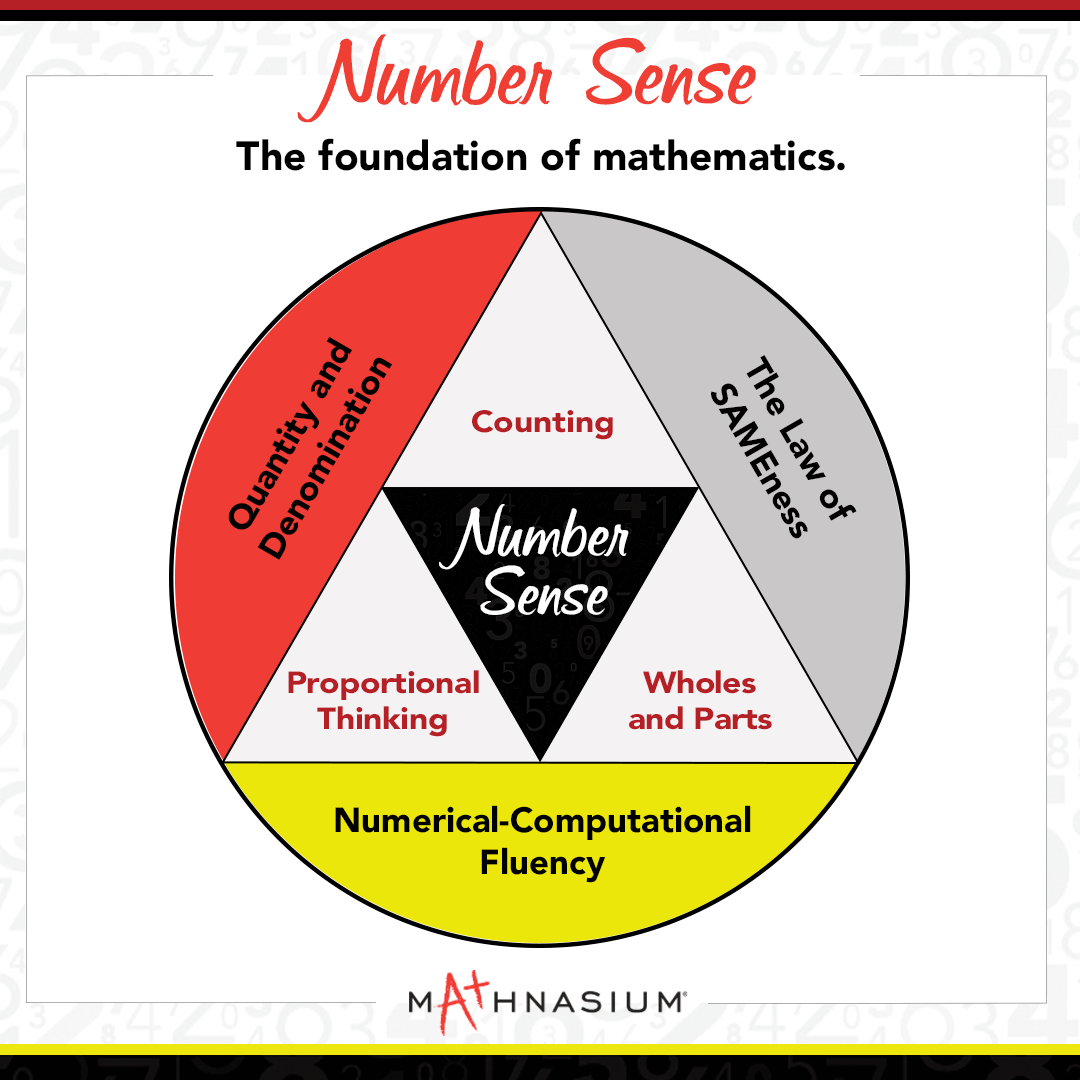
Generally, we break down number sense into three basics: counting, wholes and parts, and proportional thinking. But there are three other principles/skills that are important to fully possess number sense. We’ll break them all down here:
Counting
When children fully understand counting, they can count from any number, to any number, by any number, both forward and backward. This may sound basic — like any child would eventually learn this ability, but truly, it’s not. That’s why so many children are still using their fingers to count long past when they should be doing the math in their head (mental math).
Wholes and Parts
We all know the principle “The whole equals the sum of its parts.” A full comprehension of this principle leads to success with problem-solving and fractions — the nemesis of many children (and many adults, too).
Proportional Thinking
Proportional thinking is thinking “according to amount.” It’s a sense of scale. It helps children to understand problems such as: Five is what part of 15? If you can buy 3 candies with $2, how many candies can you buy with $10? Children who have learned proportional thinking can answer these questions quickly and easily.
Quantity and Denomination
The quantity is the amount of something — the number of things. The denomination is the name-value of that thing. In order to solve math problems, you need to know both.
The “Law of SAMEness”
This leads to Mathnasium’s “Law of SAMEness”: We can add and subtract only things that have the same name (same denomination). Here’s the classic Mathnasium example: When you add two bananas and three apples, do you get five banapples? Of course not. You can, however, get five pieces of fruit. “Fruit” is the denomination (name) that both apples and bananas share.
Numerical-Computational Fluency
Numerical fluency is the ability to “effortlessly recall — to know by heart.” While memorization is the way that many of us learned, it does notteach the mathematical thinking and problem-solving skills that are needed to build higher-order math skills. A student may memorize their 12 times tables, but a numerically fluent student uses computational strategies to quickly and efficiently answer questions beyond what is considered normal. For example, a student with numerical fluency can solve problems like 14 x 12 = ? without the need for pencil and paper.
We like to say: “It is fairly easy to forget that which you have memorized, and it’s nearly impossible to forget that which you have learned.”
Mathnasium places enormous emphasis on number sense because it truly is the key to mathematical understanding. In partnership with schoolteachers and parents, the expert math instructors in our centers grow and build upon the power of number sense to foster true conceptual understanding in children. That critical understanding leads to math mastery and to a love and appreciation of math that will positively impact their entire lives.



 (714) 731-1700 (text)
(714) 731-1700 (text)