Pascal's Triangle Patterns

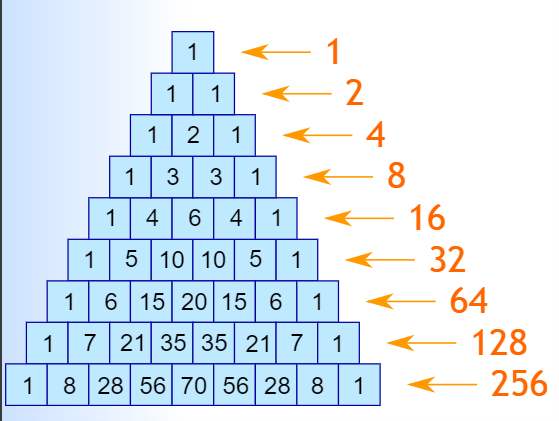
Pascal’s Triangle is simple idea that plays a important role in many different branches of math and science. It was named after a French Mathematician from the 17th century named Blaise Pascal but was used in China up to 300 years before he was born. It starts with the number one at the top and then you get each row’s numbers by adding the numbers from directly above them. You also have to make sure the first and last number of each row stays as a one so the first few rows of the triangle looks like this.

For as easy as it is to make, there are a few cool patterns that show up for seemingly no reason. One of the patterns that shows up are the exponents of 2. If you add up all the numbers in each row you get 2 raised to the power of whatever row. If you let the first row be the zeroth row, then 2^0 = 1, which is the only number in that row. Then for the first row you have 1+1 = 2 which is the same as 2^1. Then the second row is 1 + 2 + 1 = 4, or 2^2. This ends up being true if you end up picking any row but the first 9 are shown below.

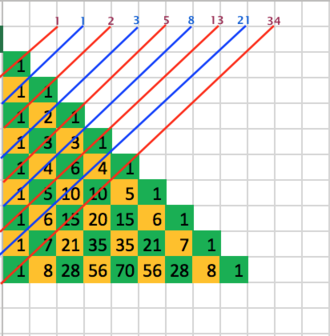
Another pattern that shows up is the Fibonacci Sequence. This happens when you add up the numbers on a diagonal instead of in a row as shown below.

There are some more places that this shows up for in higher level math like binomial expansion or combinations and permutations. One fun thing you can do is instead of making a Pascal Triangle, you can make a Pascal Pyramid and make it go up in 3 Dimensions