Have you ever heard your child or another student talk about math class and say, “That stuff doesn’t make sense to me!”? That’s pretty typical these days and it’s because children are not taught number sense. According to a 2017 article in Huffington Post, number sense is the most important mathematical concept in the 21st-century.
What is Number Sense?
Number sense essentially refers to a student’s fluidity and flexibility with numbers according to an article written by Russell Gersten and David Chard. A child with number sense has sense of what numbers mean, understands their relationship to one another, is able to perform mental math, understands symbolic representations, and can use those numbers in real world situations. In her book, About Teaching Mathematics, Marilyn Burns describes students with a strong number sense in the following way: “[They] can think and reason flexibly with numbers, use numbers to solve problems, spot unreasonable answers, understand how numbers can be taken apart and put together in different ways, see connections among operations, figure mentally, and make reasonable estimates.”
Here at Mathnasium of Parker, we compare number sense to swimming. When a child first encounters the water, they are often intimidated and afraid. They may go in but not put their head under water, or they'll walk on their tippy toes just as far as they can tilt their head back and still have their nose out of the water. However, once they've had swimming lessons and have spent a summer at the pool or beach, they gain confidence with their new abilities and are soon diving under the water and swimming all over the place. That ease and comfort is what having number sense is like in math.
The National Council of Teachers in 1989 identified the following five components that characterize number sense:
- Number meaning
- Number relationships
- Number magnitude
- Operations involving numbers and referents for number
- Referents for numbers and quantities
Why Is Number Sense Important?
Number sense is important because it encourages students to think flexibly, there are multiple ways to arrive at the correct answer, and it promotes confidence with numbers—they “make friends with numbers” as Carlyle and Mercado charmingly refer to it in their book Teaching Preschool and Kindergarten Math. Students come to understand that numbers are meaningful and outcomes are sensible and expected according to Marilyn Burns in her 2007 book, About Teaching Mathematics: A K-8 Resource. Conversely, kids who lacka strong number sense have trouble developing the foundation needed for even simple arithmetic mu ch less more complex math.
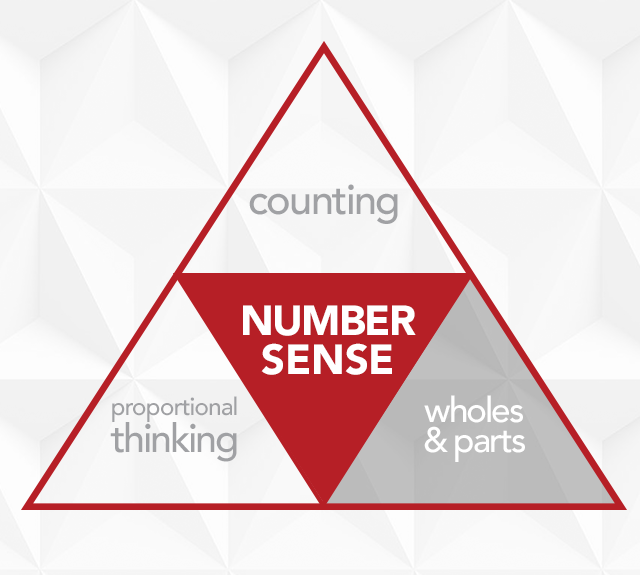
According to Mathnasium's founder and the education department in Los Angeles, number sense is the beginning of all math ability. At Mathnasium of Parker there are three main components to developing number sense: counting, wholes & parts and proportional thinking.
Teaching Strategies to Build Students’ Number Sense
We know from a wide body of research that number sense develops gradually and over time resulting from an exploration of numbers, visualizing numbers in a variety of contexts, and relating to numbers in different ways.
About Teaching Mathematics. A K-8 Resource, 3rd Edition, Marilyn Burns (2007) highlights the following key, research-based teaching strategies to build numbers sense:
- Model different methods for computing:
When a teacher publicly records a number of different approaches to solving a problem–solicited from the class or by introducing her own—it exposes students to strategies that they may not have considered. As Marilyn Burns explains, “When children think that there is one right way to compute, they focus on learning and applying it, rather than thinking about what makes sense for the numbers at hand.” An example I use frequently with parents and students is one of the verbal questions I ask upper elementary and older students during their assessment, "What is 25% of 16?" Most children who have learned the standard algorithm will use their paper and pencil and write down 16 x .25 and start multiplying. I let them get part way through before telling them to stop and asking if they want to know a trick? Unanimously, they say "yes!" and I ask them to consider what fraction 25% is equivalent to. If they have an understanding of fractions, they'll consider for a moment and say something like, "hmm?, 25% . . . 1/4 oh! it's 4! The answer is 4!"
- Ask students regularly to calculate mentally:
Mental math encourages students to build on their knowledge about numbers and numerical relationships. When they cannot rely on memorized procedures or hold large quantities in their heads, students are forced to think more flexibly and efficiently, and to consider alternate problem solving strategies. This is why every student at Mathnasium of Parker has mental math pages and are encouraged to use mental math and to begin discerning when it is appropriate to use mental math and when it is not as useful.
- Have discussions about strategies for computing:
Discussions about strategies help students to crystalize their own thinking while providing them the opportunity to critically evaluate their classmates’ approaches. Mathnasium instructors are trained in and review strategies for Socratic questioning which helps students express and describe the process and thinking they use to arrive at their answers.
- Make estimation an integral part of computing.
Most of the math that we do every day—deciding when to leave for school, how much paint to buy, what type of tip to leave in a restaurant, which line to get in at the grocery store relies not only on mental math but also on estimations. However traditional textbook rounding exercises don’t provide the necessary context for students to understand estimating or build number sense. To do that, estimation must be embedded in problem situations.
- Question students about how they reason numerically.
Asking students about their reasoning—both when they make mistakes AND when they arrive at the correct answer—communicates to them that you value their ideas, that math is about reasoning, and, most importantly, that math should make sense to them. Exploring reasoning is also extremely important for the teacher as a formative assessment tool. It helps her understand each student’s strengths and weaknesses, content knowledge, reasoning strategies and misconceptions.
- Pose numerical problems that have more than one possible answer:
Problems with multiple answers provide plenty of opportunities for students to reason numerically. It’s a chance to explore numbers and reasoning perhaps more creatively than if there was “one right answer.”
In Gersten and Chard's article the authors state, “Just as our understanding of phonemic awareness has revolutionized the teaching of beginning reading, the influence of number sense on early math development and more complex mathematical thinking carries implications for instruction.”
This is why teaching number sense is goal 1 at Mathnasium. What are our other goals when working with your child in math? Stop by and ask! We'd love to share and answer your questions!
Is Mathnasium right for your child? Call us at 303-280-6284 to find out.
Resources and articles:
Gersten, R., and D. Chard. “Number Sense: Rethinking Arithmetic Instruction for Students with Mathematical Disabilities.” The Journal of Special Education 33.1 (1999): 18-28. Print.



 303-280-6284
303-280-6284






