Brahmagupta: The Man Who Defined Zero
By Lillie Therieau
While not much is known about the life of ancient Indian mathematician Brahamagupta, his contributions to math, astronomy, and science have shaped the modern world. He was one of the first mathematicians to explore the properties of the number zero, and the first to record his ideas about it in writing.
He’s also credited with important astronomical discoveries like the fact that the Moon is closer to Earth than the Sun. Remarkably, he set his complex math and science ideas out in a book composed entirely in metered poetic verse!
Learning about this extraordinary thinker, you’ll be shocked at the number of discoveries he made that inform our everyday lives. You’ll also get an underrepresented peek into the world of ancient Indian mathematicians and astronomers, whose prolific work put the ancient Greeks to shame.
The Mysterious Life of Brahmagupta
Unfortunately, not much is known about the details of Brahmagupta’s personal life. The only surviving records which describe him focus mainly on his mathematical and scientific contributions. However, we do know that Brahmagupta was born in 598 CE in Bhillamala, in the Gurjaradesa region of India. He was a Hindu, and a Shaivite specifically. Shaivism is still one of the largest denominations of Hinduism and adherents worship the god Shiva as the supreme ruler.
Bhillamala was the capital of the Gurjaradesa region and one of the biggest cities in India at the time. It was a beacon for academics throughout the region, attracting scientists and mathematicians in particular. Brahmagupta became an astronomer himself, studying from notable Indian astronomers and texts. He also studied the five traditional Siddhantas that dealt with astronomy.
A Siddhanta is a special concept in ancient Indian culture and refers to books setting out the highest, most settled, and respected views on any particular subject. Indian astronomy already had accumulated 6 Siddhantas by the time Brahmagupta began studying astronomy.

An ancient sundial
India was one of the first and most prolific ancient cultures to deal with the movements of the stars and planets. Ancient astronomers used rudimentary tools like a sun staff or the equivalent of a modern sundial to work out enormously complex equations that dictated the placement of celestial bodies.
At the age of 30, Brahmagupta finished his first treatise, the Brahmashuptasiddhanta. The name of his treatise translates to the “improved Brahma Siddhanta”. Many believe that it is a revised version of one of the Siddhantas that he would have studied as a younger student. His work introduced many new concepts and ideas, both relating to astronomy and pure mathematics. Plus — it was even in metered verse!
Bhramagupta moved to Ujjain near the end of his life, where he published his last major treatises, the Khandakhadyaka and the Grahanarkajnana at age 67. He was the head of the astronomical observatory in Ujjain, which became the most important city for Indian astronomers in Central India. He died a few years later.
A diagram of the Earth, Moon, and Sun
Brahmagupta’s Mathematical Work
Brahmagupta was primarily an astronomer, though much of his work in that field spilled into mathematics. For instance, he discovered that the Earth was closer to the Moon than the Sun. Brahmagupta deduced this from geometry, interpreting the angles of the light and shadows created by the Sun and how the Moon appeared to wax and wane. He also calculated the exact length of a year and the circumference of the Earth with surprising accuracy.
However, Brahmagupta’s most long-lasting discoveries were in algebra, number theory, and geometry. He introduced many groundbreaking algebraic ideas in his Brahmasphutasiddhanta, including the solution to the general linear equation and the general quadratic equation. The general linear equation solution to an equation like bx + c = dx + e, is one that we all learn early in our education. However, you probably didn’t know that you have Brahmagupta to thank!
He explained that an equation like bx + c = dx + e had to be solved by isolating the variables on one side of the equation. You simply subtracted the integers from one side and added them to the other, then did the same with the coefficient/variable pairs. Finally, you would divide both sides by the leftover coefficient. Any answer would be in the form of a=x, giving you a solution!
Brahmagupta was also the first mathematician to put fractions in the visual form that we think of today. In the Brahmasphutasiddhanta, he explains how to add, subtract, multiply, and divide fractions. Brahmagupta also demonstrates how to give the sum of squares and cubes of n integers. Both of these advances were very new in the field of arithmetic and inspired the students who came after him and studied his work.
In the field of geometry, Brahmagupta pioneered the aptly named Brahmagupta formula, which allows one to solve the area of a cyclic quadrilateral. He also worked through complex calculations in triangle geometry and solved for the value of Pi within a small margin of error.
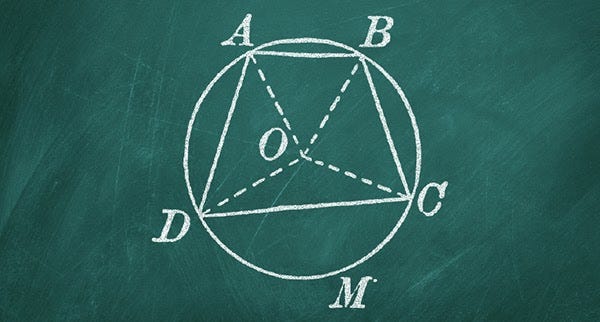
A cyclic quadrilateral
Despite the many amazing accomplishments listed already, Brahmagupta is best remembered for his work defining the number zero. Zero had already been invented in Brahmagupta’s time, used as a placeholder for a base-10 number system by the Babylonians and as a symbol for a lack of quantity by the Romans. However, Brahmagupta reimagined the identity of zero: seeing it as a number on its own, rather than a simple symbol or placeholder.
He lays out the rules for arithmetic when using zero, although his rules for division differ from our understanding today. When Brahmagupta attempted to divide 0 by 0, he came to the sum of 0. However, most modern mathematicians would argue that 0 divided by 0 is undefined. Despite this outlier, the rest of Brahmagupta’s grasp on the number zero is exactly how we conceptualize it today.
Thanks to the continued prevalence of ancient Indian mathematicians, Brahmagupta’s ideas spread all over the world. Today, we use many of the rules that he developed in his treatises as fundamental building blocks for our mathematical understanding!










