The Pythagorean Theorem is one of the most well known formulas in all of Math. It is a way of relating the two smaller sides of a right triangle to its longest side, the hypotonuse. The Pythagorean theorem states "The sum of the areas of the two squares on the legs (a and b) equals the area of the square on the hypotenuse (c)" which is more commonly known as a^2 + b^2 = c^2. But where it comes from may not be as widely known.
There have been over 350 different ways discovered to prove the Pythagorean
Theorm over the years and some of them were even developed before Pythagoras was even born all over the world in China, India, Babylon, and Egypt. However the proof that Pythagoras came up with came to him while staring at square tiles on a palace floor. In the picture below we can see what Pythagoras saw when thinking up this formula. In this picture, if we count the number of small triangles in each of the two smaller squares they will be equal to the number of small triangles in the larger square. Therefore the area of the two smaller squares added together will equal the area of the larger square which is exactly what the Pytagorean Theorem says!
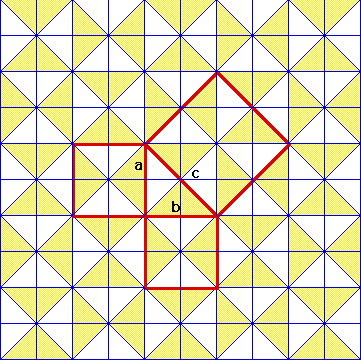
While this will always work for right triangles what would happen if we wanted to measure the length of a side if it comes off of the page like in the cube below? What do you think the length from A to D (AD) is in the cube?
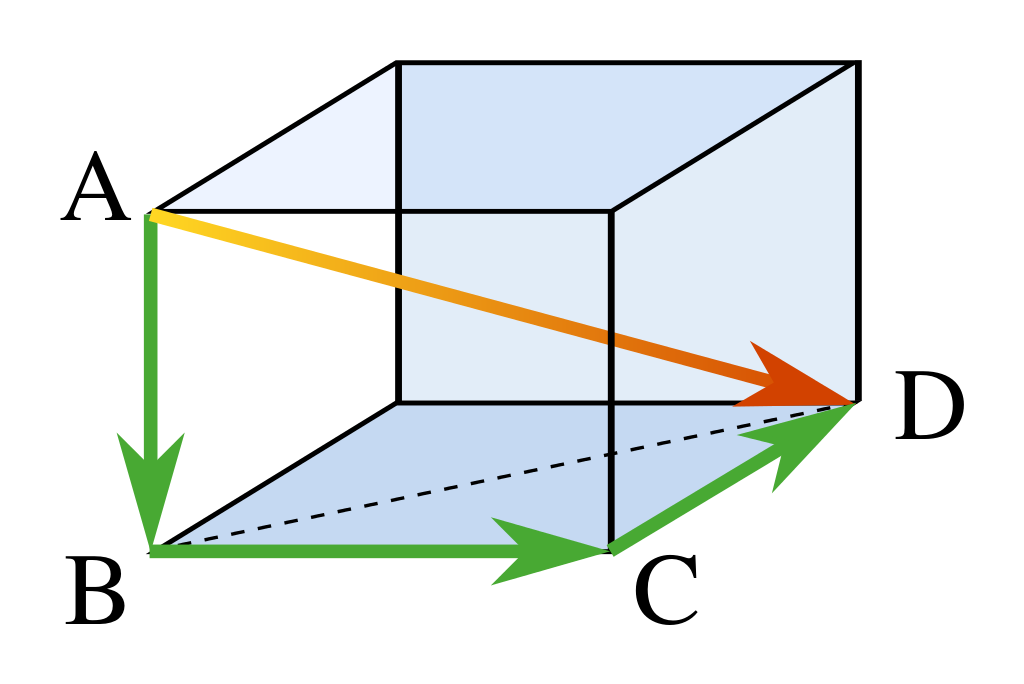
Since we already have proven the Pythagorean Theorem let's put it to use! We
can break this up into two different right triangles, one that goes across the bottom (BCD) and one that cuts vertically across the cube (ABD). For the bottom triangle we can say BC^2 + CD^2 = BD^2 and for the other triangle we have AB^2 + BD^2 = AD^2. We know what BD^2 is from our first formula so if we plug our first formula into the second one we end up with AB^2 + BC^2 + CD^2 = AD^2. This looks just like our original Pythogrean Theorem but with an extra side!













