Geodesic Domes

The spherical dome is an efficient way of enclosing space since a sphere holds a higher volume than any other container with the same surface area. In 1947, R. Buckminster Fuller patented the geodesic dome, a framework made by joining straight pieces of steel or aluminum tubing in a network of triangles. A thin cover of aluminum or plastic is then attached to the pipe.

The segments forming the network are of various lengths, but the vertices are all equidistance from the center of the dome so that they lie on a sphere. When we follow a chain of segments around the dome, we find that they approximate a circle on this sphere, often a great circle. It is this property that gives the dome design its name: a geodesic on any surface is a path of minimum length between two points on the surface, and on a sphere, these shortest paths are arcs of great circles.

Though the geodesic dome is very light and has no internal supports, it is robust and standardized parts make the construction of the dome relatively easy. Domes have been used with success for theaters, exhibition halls, sports arenas, and greenhouses.

The united states pavilion that fuller designed for Expo'67 in Montreal uses two domes linked together the 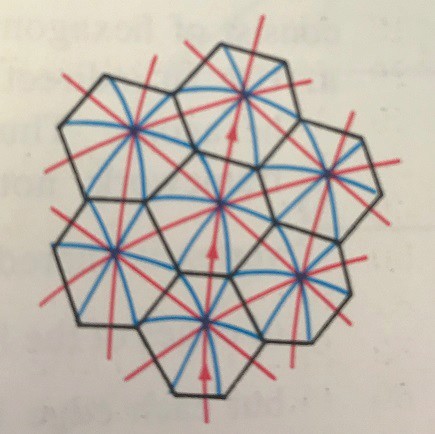design of this structure is illustrated at the right. The red triangular network is the outer dome, the back hexagons form the inner dome., and the blue segments represent the trusses that tie the two domes together. The Arrow marks one of the many chains of parts that form arcs of circles on the dome. You can see all of these features on the structure if you see inside the dome.

Although the grid of hexagons will interlock nicely to cover the plan, they cannot interlock to cover the sphere unless twelve of the hexagons are changed to pentagons. You can apply math to find out why?

Reference
[1]Geometry by Ray C.Jurgensen, Richard G. Brown, John W. Jurgensen